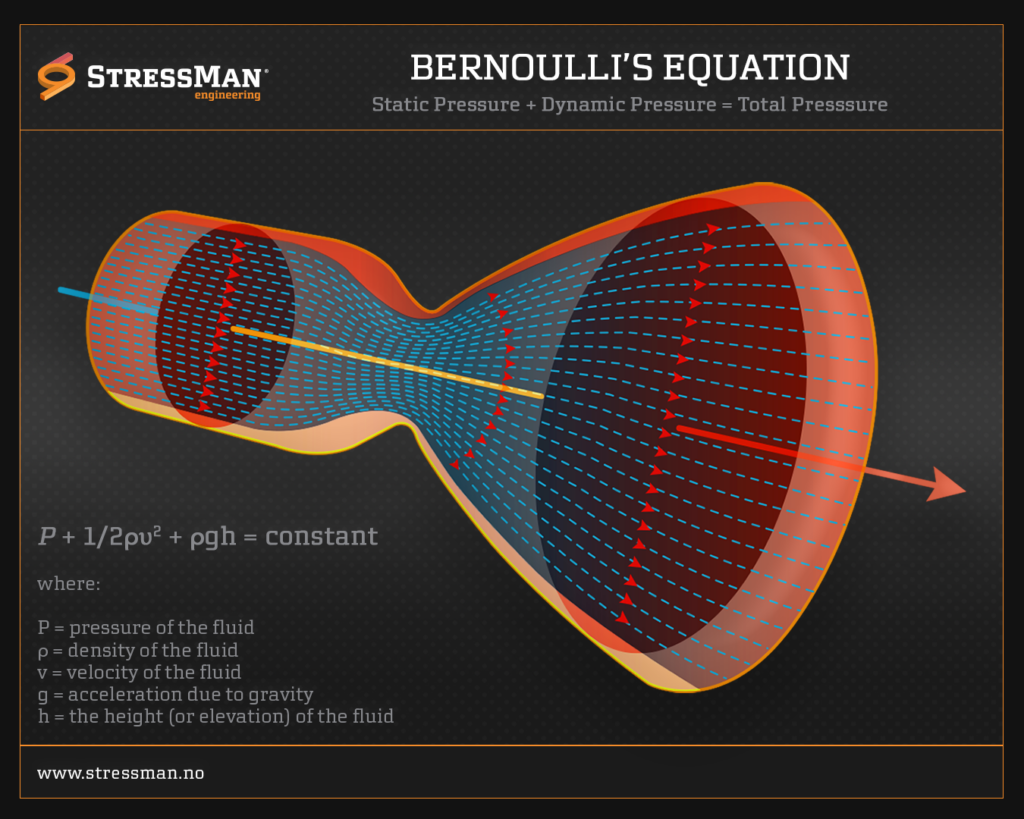
Bernoulli’s theorem, named after the Swiss mathematician and physicist Daniel Bernoulli, is a fundamental principle in fluid dynamics. It relates the pressure, velocity, and gravitational potential energy of a fluid along a streamline. The theorem is derived from the principle of conservation of energy applied to a flowing fluid. Bernoulli’s theorem is valid for incompressible and inviscid (frictionless) fluids, such as ideal liquids.
The roots of Bernoulli’s theorem lie in the conservation of mechanical energy for a fluid element moving along a streamline. The theorem is based on the idea that the total mechanical energy of the fluid remains constant along the streamline in the absence of external work or energy transfer.
Uses of Bernoulli’s theorem (subject to limitations as listed below):
1.- Fluid flow in pipes:
Bernoulli’s theorem can be used to understand fluid flow in pipes and determine the relationship between pressure, velocity, and elevation in various sections of the pipe. It finds applications in plumbing, engineering, and fluid transport systems.
2.-Aircraft aerodynamics:
Bernoulli’s theorem plays a crucial role in understanding the lift generated by an aircraft’s wings (up to a point). As air flows over the curved surface of the wing, its velocity increases, resulting in a decrease in pressure according to Bernoulli’s equation. This pressure difference between the upper and lower surfaces of the wing creates lift, allowing the aircraft to fly.
3.- Venturi effect:
The Venturi effect is a phenomenon in which the velocity of a fluid increases as it passes through a constricted section of a pipe. According to Bernoulli’s theorem, as the velocity increases, the pressure decreases. This effect is utilized in applications like carburetors in internal combustion engines and flow meters.
4.- Fluid dynamics:
Bernoulli’s theorem is widely used in various fluid dynamics applications, such as analyzing flow in nozzles, diffusers, and pumps, as well as calculating flow rates and pressure distributions in fluid systems.
5.- Weather patterns:
Bernoulli’s theorem is applied in meteorology to explain and predict certain weather phenomena, such as the formation of high and low-pressure systems and the behavior of wind flows around obstacles.
It is important to note that Bernoulli’s theorem has limitations and assumptions. It applies to steady flow along a streamline, neglects factors such as viscosity and compressibility, and assumes no energy losses due to friction or heat transfer. In real-world scenarios, these factors need to be considered for a more complete fluid dynamics analysis.