Will it buckle? 

When subject to compression loads, slender beams might buckle, leading to potential catastrophic failures in critical structures. One way to determine the critical buckling load for an idealized member is by utilizing Euler’s elastic buckling formula.

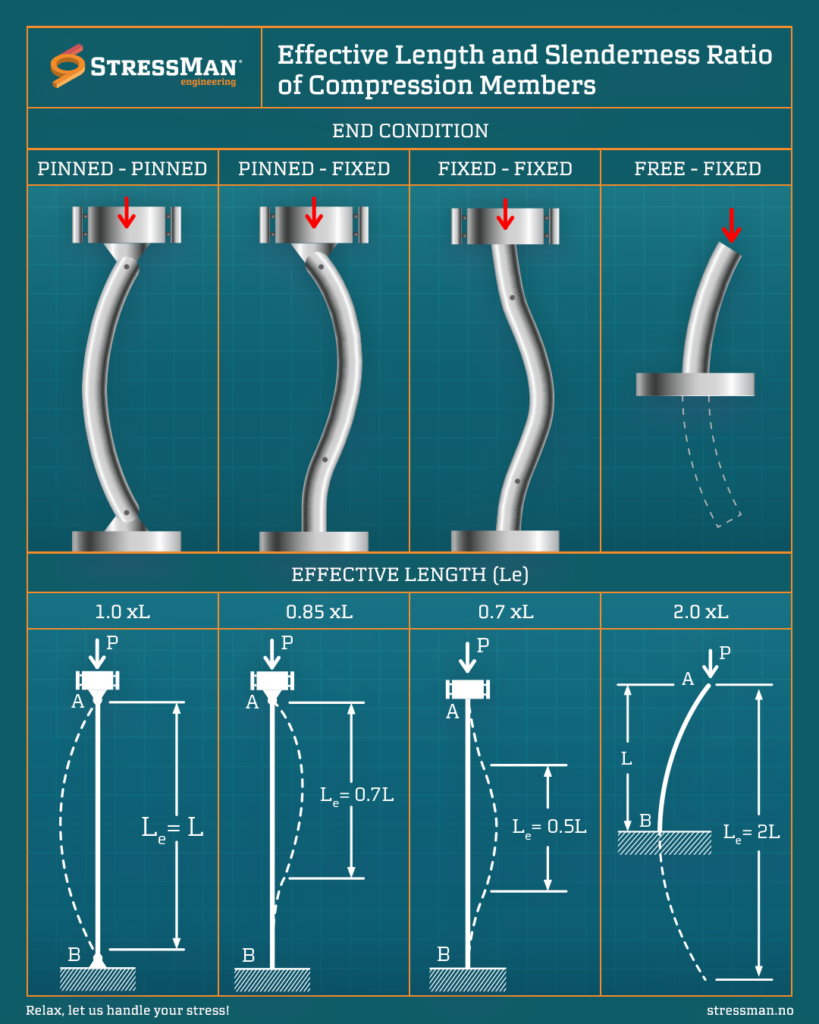
Pcr = (E*I*π^2) / ((K*L)^2)

The formula shows the relationship between E – elasticity modulus, I – moment of inertia, K – buckling length factor (see illustration), and L – the length of the member.

However, it’s crucial to note that Euler’s formula is based on idealized conditions. Real-world applications will often require adjustments. Renowned codes and regulations, such as AISC and Eurocode, incorporate imperfection factors. These factors vary based on the profile type and manufacturing method and must be considered. In many, if not most situations, the buckling load is lower than the stress criteria typically associated with beams.

When conducting Finite Element Analysis (FEA), this understanding is vital. A structural member in compression might have low-stress levels but could still be vulnerable to buckling if it’s slender. Therefore, when utilizing FEA, ensure at least an elastic buckling analysis is conducted. The results must be correlated to relevant factors of codes and regulations.